Wie funktionieren Infektionsmodelle?
In Zeiten von Corona sind Politik und Gesellschaft besonders auf eine enge Verzahnung mit der Wissenschaft angewiesen. Bereits einfache Infektionsmodelle bieten einen spannenden Einblick in die Dynamik von Epidemien. Daran wird auch deutlich, dass komplexe gesellschaftliche Herausforderungen transdisziplinäre Forschung brauchen. Epidemiologie ist schwierig. Nein wirklich, so richtig kompliziert. Dass ich mich als Physiker an einem Kurzabriss zu einem wichtigen epidemiologischen Modell versuchen möchte, kann nicht darüber hinwegtäuschen. Was aber Physik und Epidemiologie gemeinsam haben, ist der Umgang mit mathematischen Modellen. Für ein grundsätzliches Verständnis dieser Modelle beschäftigen wir uns mit drei Aspekten: der logischen Struktur, dem Anwendungsbereich und seinen Grenzen.
Von Töpfen und Trichtern
Im Folgenden betrachten wir eine einfache Form des SEIR-Modells zur Ausbreitung von Infektionen. Ausgangslage sind vier Gruppen: Menschen, die angesteckt werden können (susceptible – S), Angesteckte, die noch nicht infektiös sind (exposed – E), Infizierte, die andere anstecken können (infectious – I) und Genesene, die immun sind (recovered – R).
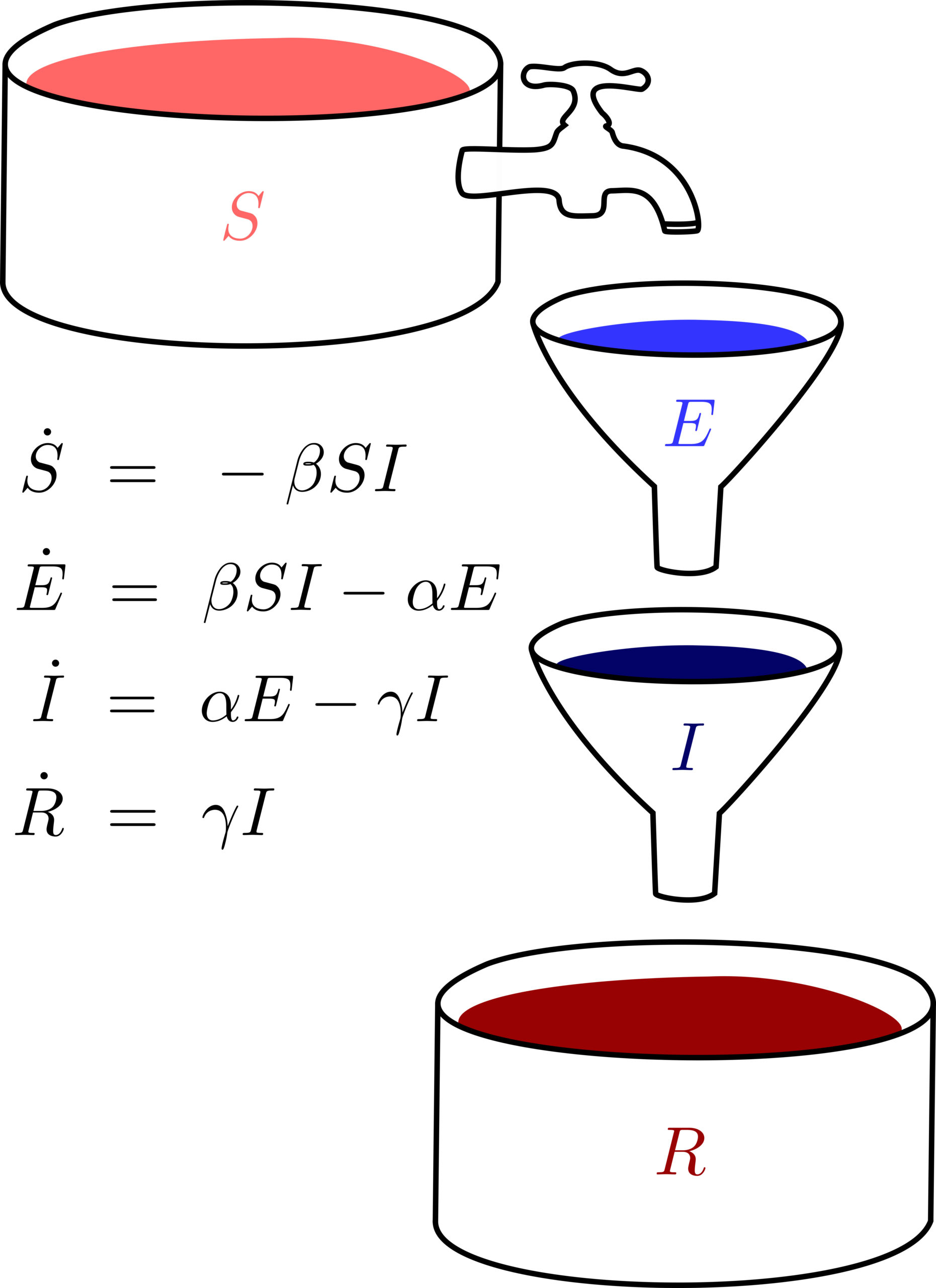
Abbildung 1 verdeutlicht diese Gruppen als Flüssigkeiten in Behältern. Dadurch wird auch klarer, wie die zeitliche Entwicklung zwischen diesen Gruppen abläuft. Wer aus dem großen Topf der Anfälligen S angesteckt wird, verbringt einige Zeit bei den Angesteckten (zuerst E, dann I) und wird schließlich gesund und immun R. Das Modell ist gerichtet. Nach der Ansteckung folgen zwangsläufig auch die anderen Stadien. Wobei Sterben, aufgrund der Krankheit oder anderer Ursachen, nicht abgedeckt ist. Eine mögliche Implementierung wäre, dass die Trichter und Töpfe lecken.
Die Ansteckung von Anfälligen ist dargestellt durch einen Wasserhahn. Das besondere an diesem Übergang ist, dass er sowohl von der Zahl der Anfälligen S als auch von den Infektiösen I abhängig ist. Erst durch den Kontakt von Anfälligen und Infizierten kommt es zur Ausbreitung der Infektion. Dann entwickelt das System eine Eigendynamik bzw. Feedback-Schleife. Die aktuellen Strategien des Social Distancing versuchen an genau dieser Stellschraube anzusetzen und den Kontakt zu begrenzen.
Neben der Abbildung ist die Mathematik des Modells in Form von Differentialgleichungen zu sehen. Auf der linken Seite sind die Größen mit einem Punkt gekennzeichnet. Damit ist die zeitliche Veränderung der jeweiligen Größe gemeint. Auf der rechten Seite stehen die Änderungsraten. Positive Terme bedeuten Zunahmen, negative Terme bedeuten Abnahmen der jeweiligen Größe.
Alle Anteile, die aus einem Vorrat abfließen kommen im nächsten Vorrat unverändert an. Die griechischen Buchstaben sind Modellparameter, können Konstanten sein und sind im Allgemeinen positiv. Die Besonderheit beim Prozess des Infizierens (Änderung von S) ist, wie bereits beschrieben, dass er sowohl von S als auch von I abhängig ist.
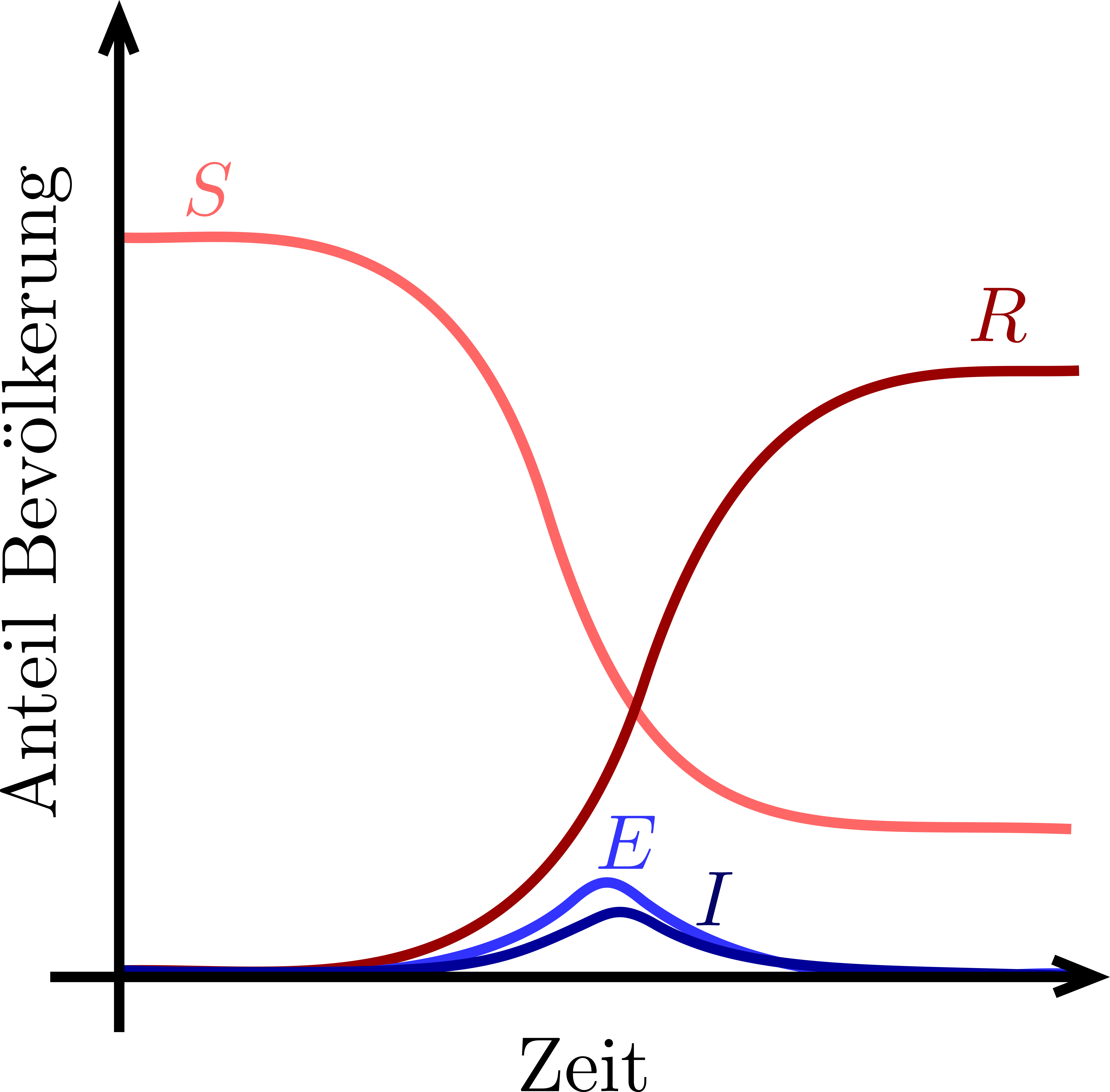
In Abbildung 2 zeigt ein schematisches Beispielszenario wie sich die Populationsanteile der vier Gruppen über die Zeit entwickeln. Dabei ist nur ein möglicher Verlauf einer beliebigen Infektionswelle nach SEIR zu sehen. Um Verwechslungen mit aktuellen Statistiken und Prognosen zu vermeiden, sind die Achsen nicht beziffert. Zu Beginn der Infektionen steigen die Anteile an Erkrankten (E und I) nur langsam. Wie in den letzten Monaten zu sehen war, ist es also schwer, den Anfang und die Gefahrenlage einer Ausbreitung einzuschätzen.
Mit der Zeit steigt aber nicht nur der Anteil an Erkrankten, sondern auch die Rate der Ansteckung, da der Anteil der Infizierten I direkt zur Änderungsrate von S beiträgt. Die Kurve wird steiler bis zu einem annähernd exponentiellen Anstieg, von dem in den letzten Wochen schon viel zu lesen war. Im gewählten Beispiel flacht danach die Kurve ab, erreicht einen Maximalwert und sinkt wieder. Zum Schluss ist die Zahl der Immunisierten so hoch, dass sich die Infektion nicht mehr stark ausbreiten kann. Da hier nur der Anteil einer Gesamtpopulation gezeigt ist, kann die absolute Zahl der Erkrankten aber immer noch sehr groß sein. Da alle Infizierten im SEIR-Modell irgendwann gesund werden, wird der Anteil der Genesenen R kontinuierlich größer. Dadurch übersteigt R bereits zu einem frühen Zeitpunkt die Anteile der Erkrankten E und I. Aus dem Verhältnis von R zu I allein lässt sich deshalb noch keine Schlussfolgerung ziehen.
Anwendungsbereich und Grenzen ausloten
Bei der Formulierung eines Modells ist immer abzuwägen, was die entscheidenden Einflüsse sind, die man verstehen will. Wie in Abbildung 1 gezeigt, betrachtet ein einfaches SEIR-Modell die Gesamtheit einer Population. Dabei wird angenommen, dass die mittlere Menge an Kontakten zwischen Menschen ausschlaggebender ist, als Schwankungen auf kleinen Skalen. Das Modell beschreibt somit ein stochastisches Verhalten einer großen Population und weniger die genaue Infektionsausbreitung zwischen einzelnen Menschen.
Damit diese Annahme gültig ist, muss die Population stark durchmischt sein und viele Kontakte zwischen Menschen ermöglichen. Um die tatsächlichen Auswirkungen von Kontroll- und Behandlungsmaßnahmen auszuloten, werden kompliziertere Modelle gewählt. Dabei können die Modellparameter beispielsweise explizit von der Zeit (Saisonalität) oder von der Art der Kontakte zwischen Menschen abhängen. Dass ein Modell nur einen begrenzten Gültigkeitsbereich hat, ist ganz natürlich. Wichtig ist es, zu verstehen, wo dieser Gültigkeitsbereich aufhört und ob das Modell von selbst Aussagen über seine begrenzte Gültigkeit trifft. Ein stochastisches Modell wie SIER mag für eine große Bevölkerung mit regem Sozialleben zutreffend sein. Zur Untersuchung regionaler Versorgungs- und Kontaktstrukturen ist es nicht geeignet. Menschen sind eben nur bedingt Tröpfchen in einer Flüssigkeit.
Die verflixten sozialen Netzwerke
Ein erster Schritt zur Untersuchung der räumlichen Ausbreitung ist die Aufteilung in einzelne Unterpopulationen. Diese folgen dann jeweils einem eigenen SEIR-Modell und stehen im Austausch miteinander. Um jedoch die Ausbreitung auf Individualebene zu verstehen, müssen Netzwerkstrukturen einbezogen werden. Mit wie vielen Menschen steht das einzelne Individuum im Kontakt? Gibt es Übertragungszentren, die von vielen Menschen besucht werden? Sind soziale Gruppen in sich abgeschlossen? Behindert oder fördert das die Ausbreitung? Bei diesen Fragen wird die Epidemiologie aus den verschiedensten Fachbereichen unterstützt – unter anderem auch aus der Physik. Mit einer großen Bandbreite an verschiedensten Methoden lässt sich die Dynamik und Komplexität dieser Systeme besser verstehen. Auf mathematischer Ebene gibt es dadurch interessante Zusammenhänge zum Verhalten von Stromnetzen, Wirtschaftssystemen oder Neuronen.
Hannes Vogel
Dieser Artikel wurde bereits im Mind Mag 136 veröffentlicht.


